ECSS Miniconference 2022

An Introduction to Probabilistic Programming in Python using PyMC

Danh Phan

Linkedin: @danhpt Twitter: @danhpt

Website: http://danhphan.net

Nov 2022

1. Introduction¶

Bayes' Formula¶

Given two events A and B, the conditional probability of A given that B is true is expressed as follows:

$$P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}$$

Bayesian Terminology¶

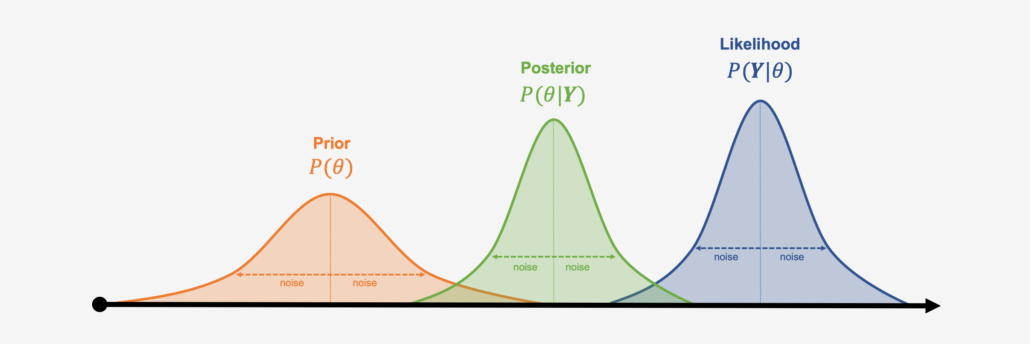
Replacing Bayes' Formula with conventional Bayes terms:

$$P(\theta|y) = \frac{P(y|\theta) \times P(\theta)}{P(y)} = \frac{P(y|\theta) \times P(\theta)}{\int P(y|\theta)P(\theta) d\theta}$$

The equation expresses how our belief about the value of $\theta$, as expressed by the prior distribution $P(\theta)$ is reallocated following the observation of the data $y$, as expressed by the posterior distribution.

1. Introduction¶

Why Bayesian Modeling?¶

  • Conceptually transparent interpretation of probablity.
  • Uncertainty quantification.
  • Allows to explicitly include prior knowledge in the model.
  • Felxible and suited for many applications in academia and industry.
  • Scalable*
Bayesian

1. Introduction¶

Why PyMC?¶

PyMC

Learn more: PyMC 4.0 Release Announcement

2. Data set¶

Anscombe's quartet is an interesting group of four data sets that share nearly identical descriptive statistics while in fact having very different underlying relationships between the independent and dependent variables.

In [5]:
plot_data()

3.1. Linear regression¶

We use the ordinary least squares (OLS) line to fit these data using NumPy's polyfit. $$y=a*x+b+ε$$

In [7]:
a_ols, b_ols = np.polyfit(x, y, deg=1)
In [9]:
plt.scatter(x, y)
plot_line(a_ols, b_ols,c='r', ls='--', label="Numpy OLS")

3.2. Robust Linear regression¶

In [10]:
is_outlier = x == 13
a_robust, b_robust = np.polyfit(x[~is_outlier], y[~is_outlier], deg=1)
In [12]:
plt.scatter(x, y);
plot_line(a_ols, b_ols, c='r', ls='--', label="NumPy OLS");
plot_line(a_robust, b_robust, ls='--', label="Robust");

4.1. Bayesian Linear regression¶

In [13]:
with pm.Model() as ols_model:
    # Priors
    a = pm.Flat("a")
    b = pm.Flat("b")    
    σ = pm.HalfFlat("σ")
    
    # Likelihood
    y_obs = pm.Normal("y_obs", a * x + b, σ, observed=y)
    
    # MCMC sampling (Default: NUTS)
    ols_trace = pm.sample(2000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a, b, σ]
100.00% [12000/12000 00:05<00:00 Sampling 4 chains, 4 divergences] 
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 6 seconds.
$$y∼Normal(a*x+b,\sigma)$$
In [14]:
pm.model_to_graphviz(ols_model)
Out[14]:
%3 cluster11 11 σ σ ~ HalfFlat y_obs y_obs ~ Normal σ->y_obs a a ~ Flat a->y_obs b b ~ Flat b->y_obs

Linear regresion: Numpy vs. PyMC¶

In [16]:
plt.scatter(x, y);
plot_line(a_ols, b_ols, c='r', ls='--', label="NumPy OLS", lw=3);
plot_line(a_bays, b_bays, c='C0', label="PyMC OLS", lw=2);

Linear regresion: posterior distributions¶

In [17]:
plt.scatter(x, y);
plot_line(a_ols, b_ols, c='C1', ls='--', label="NumPy OLS", lw=3);
plot_line(a_bays, b_bays, c='C0', label="PyMC OLS", lw=2);
# Plot many lines from posterior distributions
for a_, b_ in (ols_trace.posterior[["a", "b"]].sel(chain=0).thin(100).to_array().T):
    plot_line(a_.values, b_.values, c='C0', alpha=0.2);

Linear regresion: posterior distributions¶

In [18]:
az.plot_trace(ols_trace);
plt.tight_layout()

4.2. Bayesian Robust Linear regression¶

In [19]:
with pm.Model() as robust_model:
    # Priors
    a = pm.Normal("a", 0, 2.5)
    b = pm.Normal("b", 0., 10)    
    σ = pm.HalfNormal("σ", 2.5)
    ν = pm.Uniform("ν", 1, 10)
    
    # Likelihood
    y_obs = pm.StudentT("y_obs", mu=a*x + b, sigma=σ, nu=ν, observed=y)
    
    robust_trace = pm.sample(2000)    

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a, b, σ, ν]
100.00% [12000/12000 00:10<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 11 seconds.
$$y∼StudentT(a*x+b,\sigma, \nu)$$
In [20]:
pm.model_to_graphviz(robust_model)
Out[20]:
%3 cluster11 11 σ σ ~ HalfNormal y_obs y_obs ~ StudentT σ->y_obs ν ν ~ Uniform ν->y_obs a a ~ Normal a->y_obs b b ~ Normal b->y_obs

Robust Linear regresion: posterior distributions¶

In [22]:
plt.scatter(x, y);
plot_line(a_robust, b_robust, c='C0', ls='--', label="Robust");
plot_line(a_bays_robust, b_bays_robust, c='C0', label="PyMC OLS", lw=2);
# Plot many lines from posterior distributions
for a_, b_ in (robust_trace.posterior[["a", "b"]].sel(chain=0).thin(100).to_array().T):
    plot_line(a_.values, b_.values, c='C0', alpha=0.2);

Robust Linear regresion: posterior distributions¶

In [23]:
az.plot_trace(robust_trace);
plt.tight_layout()

5. More on PyMC¶

Examples and applications!¶

PyMC

See PyMC Documentation: Example Gallery

References¶

Theory¶

  • Statistical Rethinking by Richard McElreath
  • Statistical Rethinking in PyMC

PyMC¶

  • A Modern Introduction to Probabilistic Programming with PyMC by Austin Rochford
  • PyMC quickstart guide, tutorial, and example gallery
  • Book: Bayesian Analysis with Python
  • Book: Probabilistic Programming & Bayesian Methods for Hackers
  • Book: Bayesian Modeling and Computation in Python

Code¶

  • https://github.com/danhphan/workshops