PyMCon Web Series

An introduction to multi-output Gaussian processes using PyMC

Danh Phan

Linkedin: @danhpt Twitter: @danhpt

Website: http://danhphan.net

Feb 2023

1. Introduction¶

We have a training set D, where $$D=\{(x_i,y_i) | i=1,...,N\}$$ where $y_i$ is a scalar output, and $x_i$ is a general input vector.

All input vectors are often aggregated into a matrix $X$, and the output vector $y$ for the output values.

$$X = \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_N \end{bmatrix} y = \begin{bmatrix} y_1 \\ y_2 \\ ... \\ y_N \end{bmatrix}$$

A general model is given by $$y_i = f(x_i,\theta) + \epsilon_i$$ $$ \epsilon_i \sim N(0, \sigma) $$ For simplicity, let's assume $x_i$ is scalar.

1.1 Bayesian Linear Regression¶

$$f(x_i, \theta) = \beta_0 + \beta_1 x_i$$

where $$\theta = [\beta_0, \beta_1]$$ So $$y_i = f(x_i,\theta) + \epsilon_i = \beta_0 + \beta_1 x_i + \epsilon_i$$

The parameter $\theta$ is inferred through Bayes' rule

$$P(\theta|X,y) = \frac{P(y|X,\theta) \times P(\theta)}{P(y|X)} = \frac{P(y|X,\theta) \times P(\theta)}{\int P(y|X,\theta)P(\theta) d\theta} = posterior = \frac{likelihood * prior}{evidence \ or \ marginal \ likelihood} $$

Predict unseen data by computing the predictive posterior $$P(y_∗|X_∗,X,y) = \int P(y_∗|\theta, X_∗)P(\theta|𝐗, y)d\theta $$

1.2 Gaussian Process¶

  • The primary goal of the forecasting model is to compute the underlying function $f$ from the noisy observation $y$
  • If we less interested in $\theta$, and more interested in model predictive capability => Can infer $f$ directly!

The function $f$ is random and we need to assign a probability distribution over f

Rasmussen and Williams suggested:

*A Gaussian process is a collection of random variables, any finite number of which have a joint Gaussian distribution.*

$$\begin{bmatrix} f(x_i) \\ f(x_j) \\ f(x_k) \\ ... \end{bmatrix} = \mathcal{N}\Bigg(\begin{bmatrix} m(x_i) \\ m(x_j) \\ m(x_k) \\ ... \end{bmatrix}, \begin{bmatrix} k(x_i,x_i) & k(x_i,x_j) & k(x_i,x_k) & ... \\ k(x_j,x_i) & k(x_j,x_j) & k(x_j,x_k) & ... \\ k(x_k,x_i) & k(x_k,x_j) & k(x_k,x_k) & ... \\ ... & ... & ... & ... \end{bmatrix}\Bigg) $$

where $m$ and $k$ denote the mean and covariance functions (kernels) respectively. As an alternative way define a function that is distributed according to a Gaussian process as:

$$f(x) = \mathcal{GP}( m(x), k(x,x') )$$

1.3 GP Mean and Covariance Functions¶

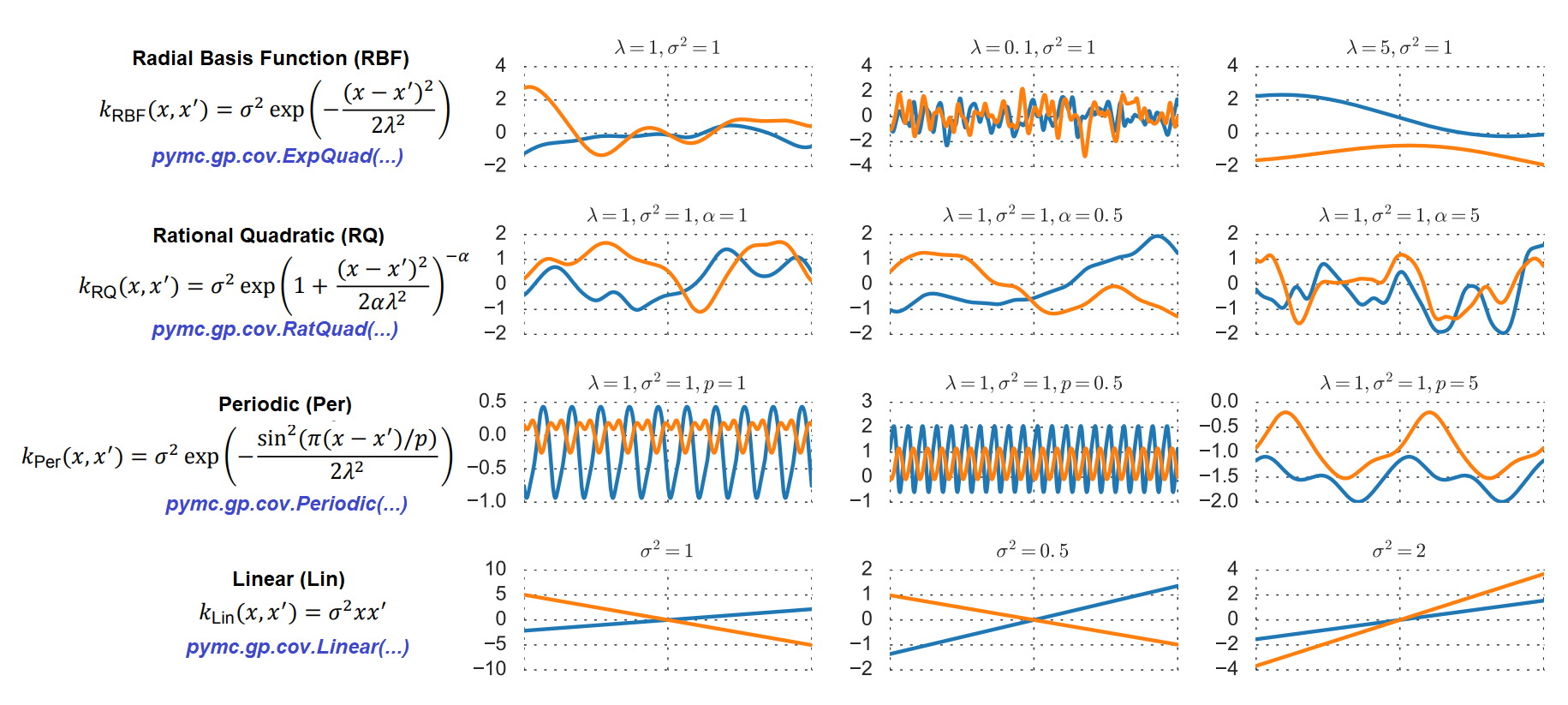
Covariance functions
  • https://www.pymc.io/projects/docs/en/latest/api/gp/cov.html
  • https://www.pymc.io/projects/examples/en/latest/gaussian_processes/GP-MeansAndCovs.html
In [2]:
# Data set
data_url = 'https://raw.githubusercontent.com/danhphan/workshops/main/2023-PyMCon/data/salmon.csv'
salmon_data = pd.read_csv(data_url)
x, y = salmon_data[['spawners', 'recruits']].values.T
print("Data shape: ", salmon_data.shape, x.shape, y.shape)
salmon_data.plot.scatter(x='spawners', y='recruits', s=50, figsize=(5,3));
plt.xlabel("x: spawners");
plt.ylabel("y: recruits");

Data shape:  (40, 2) (40,) (40,)

2. Model implementation in PyMC¶

2.1 Bayesian Linear Regression¶

Simple linear regression: $$y_i = f(x_i,\theta) + \epsilon_i$$ $$ y_i = \beta_0 + \beta_1 x_i + \epsilon_i $$

There are three unknowns, each of which need to be given a prior:

$$\beta_0, \beta_1 \sim \text{Normal}(0, 50)$$$$\sigma \sim \text{HalfNormal}(50)$$
In [3]:
# Create a PyMC model
with pm.Model() as linear_salmon_model:
    # Prior
    beta_0 = pm.Normal('beta_0', mu=0, sigma=50)
    beta_1 = pm.Normal('beta_1', mu=0, sigma=50)
    sigma = pm.HalfNormal('sigma', sigma=50)    
    mean = beta_0 + beta_1 * x
    # Likelihood
    recruits = pm.Normal('recruits', mu=mean, sigma=sigma, observed=y)
In [4]:
# Prior distribution
a_normal_distribution = pm.Normal.dist(mu=0, sigma=50)
plt.hist(pm.draw(a_normal_distribution, draws=1000));
In [5]:
# Prior distribution
a_half_normal_distribution = pm.HalfNormal.dist(sigma=50)
plt.hist(pm.draw(a_half_normal_distribution, draws=1000));
In [6]:
with linear_salmon_model:    
    linear_trace = pm.sample(1000, tune=2000, cores=2)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [beta_0, beta_1, sigma]
100.00% [6000/6000 00:03<00:00 Sampling 2 chains, 0 divergences] 
Sampling 2 chains for 2_000 tune and 1_000 draw iterations (4_000 + 2_000 draws total) took 4 seconds.
In [7]:
# Posterior distribution
az.plot_trace(linear_trace.posterior);
plt.tight_layout()
In [8]:
# Prediction
X_pred = np.linspace(0, 500, 100)

ax = salmon_data.plot.scatter(x='spawners', y='recruits', c='k', s=50, figsize=(5,3))
ax.set_ylim(0, None)
for b0,b1 in zip(linear_trace.posterior['beta_0'].sel(chain=0)[:20], 
                 linear_trace.posterior['beta_1'].sel(chain=0)[:20]):
    b0,b1=b0.values,b1.values
    ax.plot(X_pred, b0 + b1*X_pred, alpha=0.3, color='seagreen');
plt.xlabel("x: spawners");
plt.ylabel("y: recruits");

2.2 Gaussian Processes in PyMC¶

$$y_i = f(x_i,\theta) + \epsilon_i$$$$f(x) = \mathcal{GP}(m(x), k(x,x')$$$$f(x) = \mathcal{GP}( Linear, ExpQuad(x,x') )$$
In [9]:
with pm.Model() as gp_salmon_model:

    ρ = pm.HalfCauchy('ρ', 5)
    η = pm.HalfCauchy('η', 5)
    
    M = pm.gp.mean.Linear(coeffs=(salmon_data.recruits/salmon_data.spawners).mean())
    K = (η**2) * pm.gp.cov.ExpQuad(input_dim=1, ls=ρ) 
    
    σ = pm.HalfNormal('σ', 50)
    
    recruit_gp = pm.gp.Marginal(mean_func=M, cov_func=K)
    recruit_gp.marginal_likelihood('recruits', 
                        X=salmon_data.spawners.values.reshape(-1,1), 
                        y=salmon_data.recruits.values, noise=σ)
In [10]:
with gp_salmon_model:
    gp_trace = pm.sample(1000, tune=2000, cores=2, random_seed=42)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [ρ, η, σ]
100.00% [6000/6000 00:22<00:00 Sampling 2 chains, 0 divergences] 
Sampling 2 chains for 2_000 tune and 1_000 draw iterations (4_000 + 2_000 draws total) took 22 seconds.
In [11]:
az.plot_trace(gp_trace, var_names=['ρ', 'η', 'σ']);
plt.tight_layout()

Predict unseen data by computing the predictive posterior $$P(y_∗|X_∗,X,y) = \int P(y_∗|\theta, X_∗)P(\theta|𝐗, y)d\theta $$

$$P(y_∗|X_∗,X,y) = \int P(y_∗|X_∗,f,X)P(f|𝐗,y)df $$
In [12]:
# Prediction 
with gp_salmon_model:
    salmon_pred = recruit_gp.conditional("salmon_pred", 
                                        X_pred.reshape(-1,1))
    gp_salmon_samples = pm.sample_posterior_predictive(gp_trace, 
                                  var_names=['salmon_pred'], random_seed=42)

Sampling: [salmon_pred]
100.00% [2000/2000 00:11<00:00]
In [13]:
ax = salmon_data.plot.scatter(x='spawners', y='recruits', c='k', s=50)
ax.set_ylim(0, None)
for x in (gp_salmon_samples.posterior_predictive['salmon_pred']
          .sel(chain=0)[:3,:]):
    ax.plot(X_pred, x);
In [14]:
from pymc.gp.util import plot_gp_dist
fig, ax = plt.subplots(figsize=(8,6))
plot_gp_dist(ax, (gp_salmon_samples.posterior_predictive['salmon_pred']
                  .sel(chain=0)[:50,:]), X_pred)
salmon_data.plot.scatter(x='spawners', y='recruits', c='k', s=50, ax=ax)
ax.set_ylim(0, 350);

3. References¶

  • Rasmussen and Williams, 2005. Gaussian Processes for Machine Learning
  • Bagas Abisena Swastanto, 2016. Gaussian process regression for long-term time series forecasting
  • Chris Fonnesbeck, PyData NYC, 2019. A Primer on Gaussian Processes for Regression Analysis
  • Oriol Abril & Bill Engels, PyMC Examples, 2022. PyMC Mean and Covariance Functions
  • Notebook codes, Danh Phan, 2023. https://github.com/danhphan/workshops/2023-PyMCon